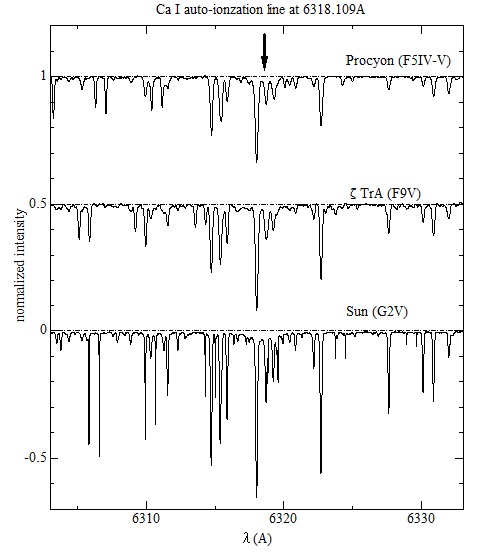
G型星やF型星のスペクトルを扱っていると、異常に広がった(4Å程度) Ca I のスペクトル線に出会うことがある。ただ、数%程度の凹みなので注意しないと気づかないほどだが、高分散で高SN比のスペクトルが取得できるようになり、比較的頻繁に目にするようになった。異様な広がりに驚くことがあるので、備忘録がてらまとめておくことにした。
Kurucz & Bell (1995) のスペクトル線リストには Ca I auto-ionization lines の注釈が下記の3本に付されている:
( )内はそれぞれ lower excitation potential(eV), log gf, g_rad, C4, C6 で、g_radはradiation damping constant, C4は quadratic Stark broadening の係数, C6は van der Waals damping の係数である。C4は、通常、-5から-6位の値が与えられているので、ここでは適正には評価されていないようである。g_rad は通常6〜9だから、11.28は大きい。C6 は-7位だからこれは小さい。
Procyon (F5IV-V)、ζTrA (F9V)、Sun (G2V)の3星の例(Allende Prieto et al. (2004) のスペクトル・データベースを用いた)を掲げる。

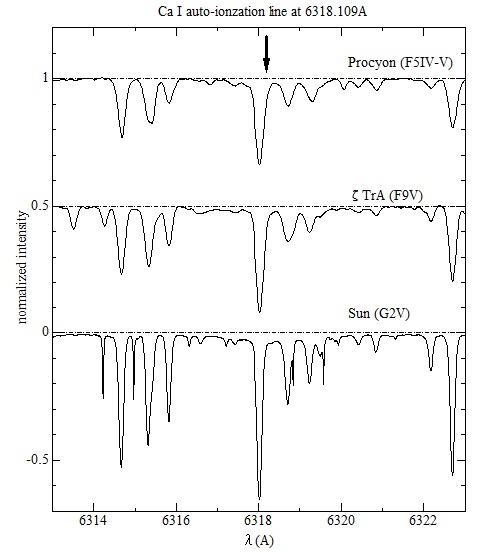
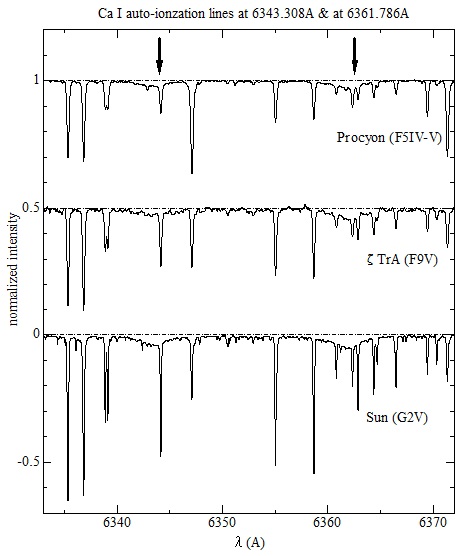
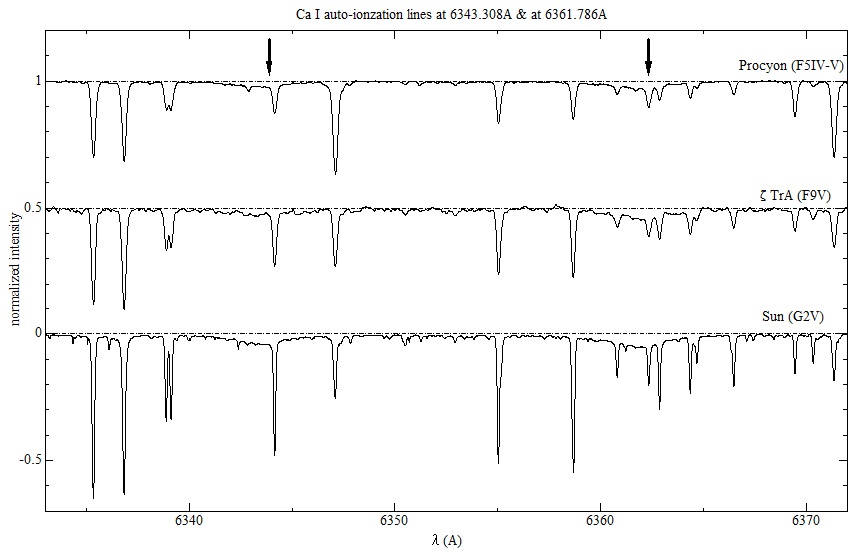
上記3本の線は上下2つのエネルギー・レベルの間の bound-bound transion で生じている。
下のエネルギー・レベルの excitation potential は4.430〜4.451eV である。
一方、上のレベルは6340A程度の波長λに相当するエネルギー分だけ高い。それを eV に換算すると(1.24×10^(-4)/λ(cm))=1.95(eV) である。すなわち、上のレベルの excitation potential はおよそ 6.4eV となっている。
ところで、Ca I の電離ポテンシャルは 6.11eV だから、ここで得られた6.4eVはなんとこの電離ポテンシャルより高く、連続部にある! 「ええ? そんなことがあってええの?」と思うのが常識だが、そんなことがあるらしい。もちろん、非常識なわけで、こんなレベルが安定に存在できるわけはなく、周囲にうごめく他の原子や電子の攻撃を受け、そのレベルは結構なエネルギー幅を持っている。そこで、この transition で生じるスペクトル線は幅の広いものになる、ということで、上の現象が説明される。
このようなプロセスが auto-ionization で、Ca I では観測されていて、Ca I が卓越しているF型星やG型星で顕著に見られる。
ヘルツベルグ(1964)の「原子スぺクトルと原子構造」のp.170に解説があるのでご覧いただきたい。
要は電子が1個だけ励起しているのではなく2個、励起しているという。この場合、1個だけの場合とエネルギーレベルが変わる(異常項と呼ぶ)。電離ポテンシャルが 6.11eVというのは電子が1個だけ励起され、他は基底状態にある場合の値であって、この場合、レベルはこれ以下に並んでいる(正常項)のに対し、異常項では 6.11eVの電離ポテンシャルを越えて存在することもできる。そこで、この異常項に遷移が起ると、すでにそこは電離ポテンシャルを越えた電離空間だから、それでそのまま電離してしまう。この場合、余分なエネルギーを加えることなく電離するので、「自動イオン化」auto-ionization である。
Kurucz & Bell (1995) のスペクトル線リストには Ca I 線が12,858本登録されている(波長域は1,372A〜999,627A)。
そのうち上下レベルが6.11eV 以下の線は5,648本で、6.11eV を越えての遷移は7,210本となっていて、異常項に関係した線の方が多い。どちらが異常か、分からない。
その異常な方の線のうちgf値が大きい順に10本書き出したのが下の表である。
今回紹介した線が3強であることが分かる。
表 Ca I 線の異常項に関係した主要な線10本
| -- | -------- | ------- | ---------- | ----- | ---------- | ----------- | ----- | --------- |
| No | WV(nm) | log gf | upper | eV | level | lower | eV | level |
| -- | -------- | ------- | ---------- | ----- | ---------- | ----------- | ----- | --------- |
| 20 | 636.179 | 0.954 | 51611.40 | 6.40 | 5 3d4d 3G | 35896.89 | 4.45 | 4 3d4p 3F |
| 20 | 634.331 | 0.845 | 51579.00 | 6.40 | 4 3d4d 3G | 35818.71 | 4.44 | 3 3d4p 3F |
| 20 | 631.811 | 0.699 | 51553.60 | 6.39 | 3 3d4d 3G | 35730.45 | 4.43 | 2 3d4p 3F |
| -- | -------- | ------- | ---------- | ----- | ---------- | ----------- | ----- | --------- |
| 20 | 760.988 | -0.198 | 51396.32 | 6.37 | 3 3d4d 3D | 38259.12 | 4.74 | 3 3d4p 3D |
| 20 | 829.218 | -0.391 | 51396.32 | 6.37 | 3 3d4d 3D | 39340.08 | 4.88 | 2 3d4p 3P |
| 20 | 760.232 | -0.408 | 51369.38 | 6.37 | 2 3d4d 3D | 38219.12 | 4.74 | 2 3d4p 3D |
| 20 | 669.102 | -0.416 | 53200.40 | 6.60 | 4 3d4d 3F | 38259.12 | 4.74 | 3 3d4p 3D |
| 20 | 817.329 | -0.546 | 51571.70 | 6.39 | 1 3d4d 3S | 39340.08 | 4.88 | 2 3d4p 3P |
| 20 | 665.206 | -0.575 | 53247.90 | 6.60 | 3 3d4d 3F | 38219.12 | 4.74 | 2 3d4p 3D |
| 20 | 830.747 | -0.631 | 51369.38 | 6.37 | 2 3d4d 3D | 39335.32 | 4.88 | 1 3d4p 3P |
| 20 | 759.707 | -0.680 | 51351.74 | 6.37 | 1 3d4d 3D | 38192.39 | 4.74 | 1 3d4p 3D |
| -- | -------- | ------- | ---------- | ----- | ---------- | ----------- | ----- | --------- |
(2013.10.15.)